Local Differential Privacy, Randomized Response, and Global DP in 10 min read
In the last 2 decades, with the increasing availability of sensors and the popularity of the internet, data has become more ubiquitous than ever. Yet, having access to personal data to perform statistical analysis is hard. In fact, that is one of the main reasons we, as data analysts, spend so much time doing research using “toy” datasets, instead of using real-world data. For areas like Healthcare, it is common to see the birth of specialized startups that spend years in contact with medical centers in order to get quality datasets.
But, what if there was a way for medical centers (or any institution) to share data, for analytical purposes, without compromising their patient’s privacy?
Let’s walk through some classic solutions for privacy preserving, explore their weaknesses, and present new ideas that are shaping a new horizon of privacy-based applications.
Data Anonymization
A world in which data is freely available is not ideal and we doubt it will be in the coming decades. Despite the growing recent cases of customer data being stolen and used for many spurious purposes by companies, the general direction points to strong regulations for usage and storage of user data. And the reason for it is very simple — people, in general, do care about their privacy.
And in the face of reality, the question we most care about is:
How can we use machine learning to solve some of the most important problems in society without compromising people’s privacy?

There are a lot of tools that do data anonymization. Also, agencies like the European Data Protection Supervisor (EDPS) and the Spanish Agencia Española de Protección de Datos (AEPD) have issued joint guidance related to requirements for anonymity. According to these agencies, no one, including the data controller, should be able to reidentify data subjects in a properly anonymized dataset.
However, there are many research publications that highlight the fragility of data anonymization — mainly in times of big data proliferation. One of the most famous cases might be the Netflix Prize.

The challenge took place is 2009 and awarded the winning team a 1-million-dollar prize for the best recommendation system. To the competitors, Netflix released an anonymized dataset containing 100 million movie ratings from half a million users.
However, shortly after that, 2 researchers from the University of Texas managed to deanonymize the data. They used cross-reference techniques, with a publicly IMDB dataset, to find users that rate movies on both platforms. As a result, they managed to identify the name of the users and movies for a big part of the database.
And that was not new! Cross-reference techniques have been used to deanonymize many other private datasets. In fact, some people in the data privacy community consider data anonymization an outdated technique that should be discouraged.
A Better Alternative
Differential Privacy (DP) is a framework designed to share information about a dataset. Different from data anonymization, DP focuses on sharing information that describes patterns within groups of people while withholding information about individuals in the dataset. In other words, if a study finds out some pattern that describes a certain person, it is not because private info about that person was leaked. Instead, it is because the pattern in question is shared across a large group of people — thus not a particular property of that specific person.
To dive into the concepts around DP, let’s work with a “toy” database example. Let’s have a database containing a single column, describing a property, and one row for each person. We can think of this property as anything. It could be the presence of a disease, or if a person is married or not. Indeed, the property does not matter much in this case.
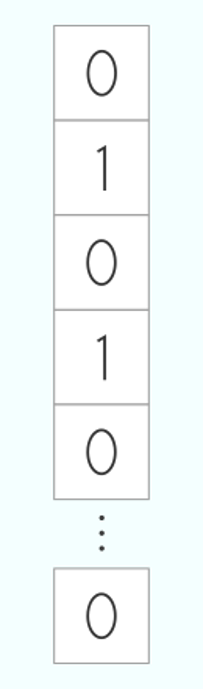
The canonical database. It contains one single column and one row for each person.
As with any other dataset, we can issue queries to it. We can, for example, calculate the sum or the mean among all people in the corpus.
Suppose the following scenario. After querying the database once, if we were to remove one person from it, and then re-run the same query, would the 2 query outputs differ? More specifically, what would be the maximum difference that could happen? Note that we need to consider the maximum over all possible situations. That is, we need to consider all possible entries/persons that could be removed from the database.
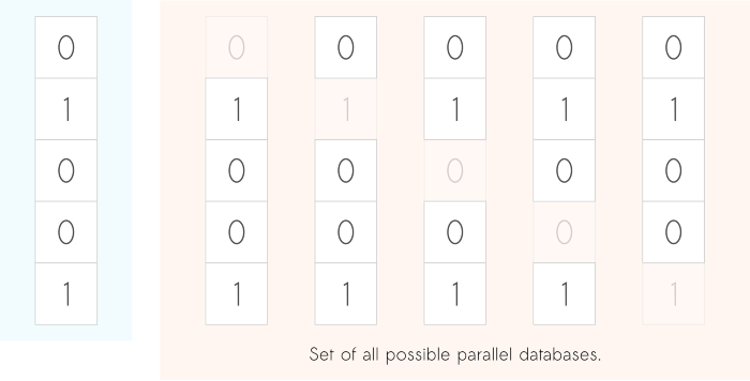
Left (in blue) the original database. Right, we show the N possible parallel/neighboring databases. These are versions of the original database with one record removed from it.
The amount by which the 2 outputs would change in the example above is called the sensitivity of the query, and it is a key concept in DP. As you might have guessed, different queries may have different sensitivities. Take the sum query as an example. Considering a toy database of size 5, the maximum change is 1 — when we remove a person with a property of 1, but it could also be 0. The mean query, on the other hand, has a much smaller sensitivity. It is roughly 1 divided by the size of the database.
Note that, we are measuring how sensitive the output of a query is if we remove someone from the data. Intuitively, if a query sensitivity is high, the query output is leaking more “private” information than otherwise. In other words, if after removing one person from the database, the output of the query does not change, it means that the person’s info (that was removed) does not contribute to the result of the query.
Noise is the Answer
It is important to note that the key ingredient to any differentially private algorithm is noise. DP is grounded on the concept that privacy cannot be protected without the injection of noise. Put it differently, DP requires some sort of randomness that must be added to the data or to the output of a query. In fact, the location where we add noise is what differentiates the 2 kinds of DP.
Local Differential Privacy
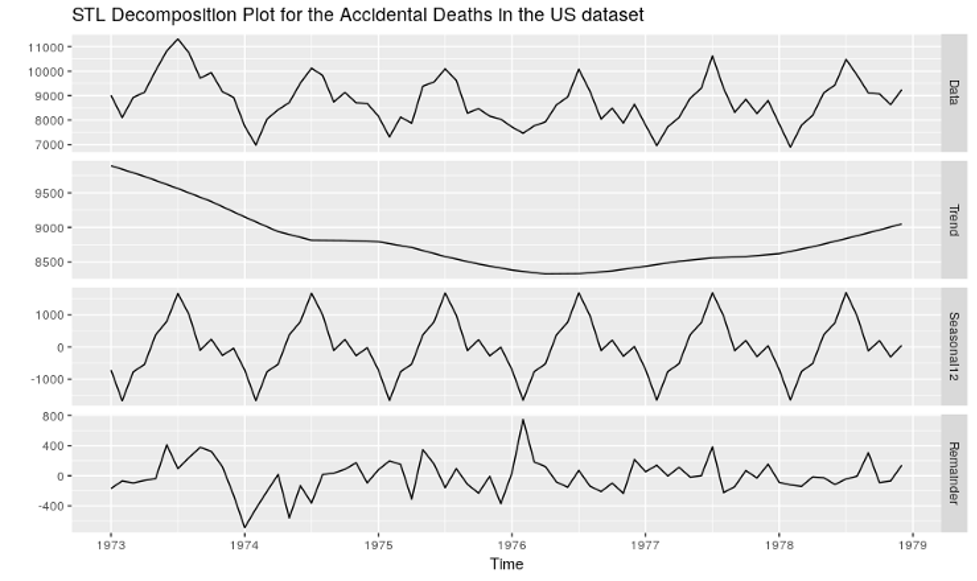
In local differential privacy, random noise is added to each individual record before it is stored in a database. As you can see, no one, even the database owner has access to the original data. Local DP is the most secure protocol. However, this high level of protection does come with a cost.
To have a clear understanding, let’s implement local DP using a technique called Randomized Response.

Local Differential Privacy pipeline. Note how the noise is added to the data before it goes to the database.
Randomized Response
In short, Randomized Response is a data collection method that ensures that only a noisy version of the true dataset is collected. Let’s take a closer look at it using a very simple protocol — Coin flipping.

https://miro.medium.com/max/390/1*kNulaZGpJi02aYqn5Q03zw.gif
Imagine we are designing a survey that seeks to understand patterns about some taboo behavior. Some example questions we might include in our survey could be:
- Have you ever stolen anything from your workplace?
- Have you ever jaywalked?
- Have you cheated on your spouse?
Well, it is easy to see that these are sensitive questions. And knowing people as we do, they will probably get uncomfortable and answer dishonestly. As a result, the data analyst, on the other end, would get skewed results.

https://miro.medium.com/max/302/0*sZxBeG79J8eEZ5Bu.gif
Randomized Response works like that. Instead of asking the question directly to someone — “Have you jaywalked?” — we shall do the following.
- Ask the respondent to take a coin and flip 2 times — no one but the respondent can see the flipping results!
- Then, you say to the participant, if the first coin flip lands Heads, I want you to answer the question honestly.
- However, if the first coin flip lands Tails, I want you to answer based on the result of the second coin flip. That is, if the second coin flip lands Heads, answer yes, otherwise, answer no.
The whole idea is to add a certain degree of randomness into the process so that the participants feel protected. And the reason they feel that way is because there is no way to trace it back, and figure out who responded yes or no honestly.
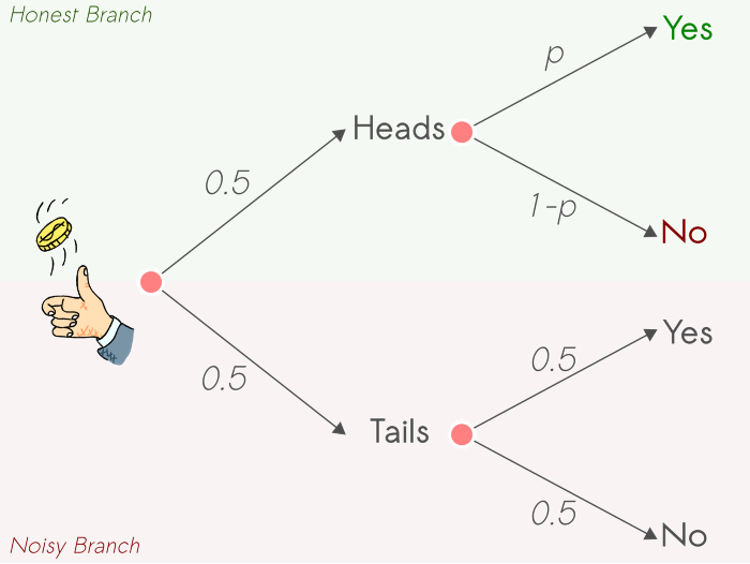
But let’s take a moment and examine what really happened with our surveys’ response distribution. For half of the questions, we will get honest responses, these can be either positive or negative. However, for the other half, individuals will answer randomly with a 50–50 chance of saying yes or no.
In practice, imagine a situation where 70% of people have stolen at least once from work (true unknown proportion). For half of the questions, people will say yes or no with a 50–50 chance. However, for the other half, they respond yes with a 70% probability. As a result, the 50–50 distribution gets averaged with the true distribution and produce a final distribution of 60%. And the beautiful thing about all this is that, since we know all the factors, except the true distribution, we can do the reverse algebra and figure out the true population statistics that we really care about. In other words, if we get a final 60% from the survey, we know that the true statistic is 70%!
And that is Local Differential privacy. Note that the private mechanisms — the noise — was added to the data before it was collected and stored. Thus, no one can see or recover information about anyone with certainty.
Note that the process of recovering the true statistics is noisy as well. In other words, the amount of noise we add comes with an accuracy tradeoff. The more the noise, the less the accuracy in which we can recover the true data distribution. Indeed, in theory, only with an infinite number of participants we would recover the true statistics. In other words, the sample size matters.
And that is where global differential privacy shines.
Global Differential Privacy
Global DP has one clear advantage over Local DP. We can add less noise, ensure privacy, and get more accurate results. Consequently, Global DP allows the use of these techniques in smaller groups of individuals without losing much accuracy. However, there is a clear downside. Since the noise is added to the output of a query, the data owner has access to the original/raw data. In other words, we need to trust the database owner.
Global Differential Privacy pipeline. Here, the noise is added to the output of the query.
But one central question in all this is, how much noise should we add? That is where the mathematical definition of Differential Privacy kicks in.

What this equation says is that, for a given query M, and databases x and y, if we run the query M on databases x and y separately, the maximum difference between the results of the 2 queries can be at most exp(ε). However, there is a probability that this inequality does not hold, which is given by δ. Note that y, is called a parallel or neighboring database. As in the example above, that would be a copy of database x, with one entry removed from it.
In short, the amount of noise depends on 4 factors.
- The type of noise we add. Two practical options are Gaussian or Laplacian Noise.
- The sensitivity of the query function. Usually, the less the sensitivity of the query, the smaller the noise we can add.
- The desired ε. Epsilon is treated as a privacy budget. It defines the amount of statistical leakage we are willing to allow per query. The smaller the epsilon, it means more noise added, and more random statistical results.
- The amount of δ. If we choose Laplacing noise, δ is zero and we can forget it.
In short, if a query has high sensitivity, it means we will need to add more noise. And for a query with small sensitivity, we need less noise respectively. The more noise we add (smaller epsilon), the more protection we add. It also means that the more randomized the recovered statistics will be, and the more data we will need to ensure good accuracy.
And that brings us to some counter-intuitive properties of Differential Privacy. Usually, people think of privacy as allowing less information about themselves to be released. With DP though, the more data we have, the more protection we can enforce, and still recover good statistics to perform analysis.
Conclusion
As countries advance in their data regulation agendas, more reliable techniques to enforce data privacy grows in importance. In this frontier, Differential Privacy gains in popularity for its solid mathematical background and practical reliability. It is already possible to use all the concepts described above, and some more, to ensure privacy in an enterprise environment. PySyft, a Python library for secure and private Deep Learning, shines among the best open-source tools out here. Hope you have enjoyed reading.Acknowledgement
This piece was written by Thalles Silva, Innovation Expert at Encora’s Data Science & Engineering Technology Practices group. Thanks to João Caleffi and Kathleen McCabe for reviews and insights.
References
[1] Kearns, Michael, and Aaron Roth. The ethical algorithm: The science of socially aware algorithm design. Oxford University Press, 2019.
[2] Udacity’s Secure and Private AI online course.
About Encora
Fast-growing tech companies partner with Encora to outsource product development and drive growth. Contact us to learn more about our software engineering capabilities.